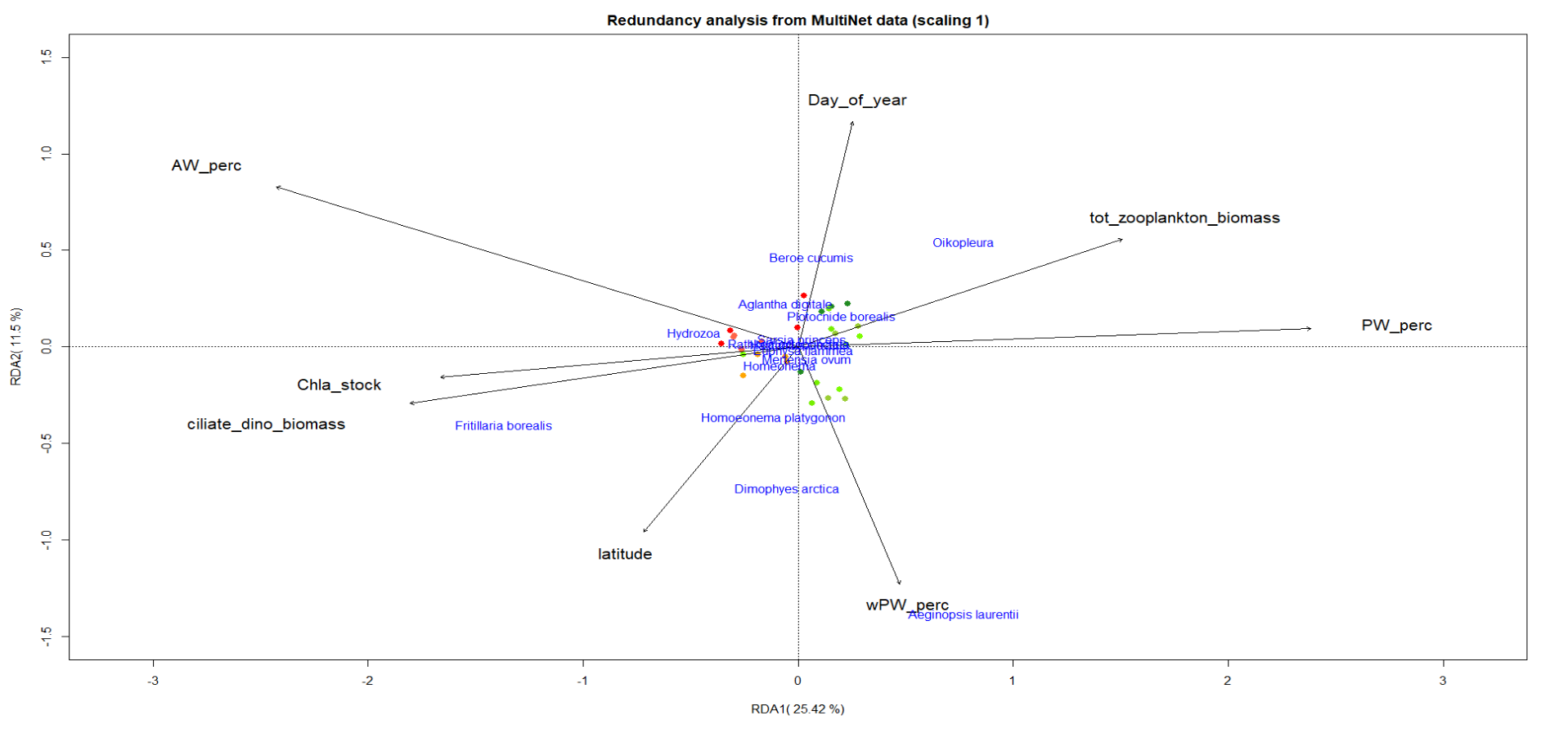
Competitive population dynamics (May-August 2024)
This project was a 4 month intership with Benoit Sarels. We tried multiple approaches to study population dynamics on heterogenous environments, using cellular automata (CA) models and PDEs models. The goal was to study and compare these two approaches when applied to a case study regarding the repartition of two competing balanoide species (Perforatus perforatus and Chtamalus sp.) on a rocky beach of Bretagne. We have shown theorically and numerically interesting traits of the CA and PDEs models we developped. Then, we applied them to the study case and produced results that are coherent to the species repartitions observed in situ.
Here is the heterogenous PDE problem we considered: Lets \(\Omega = ]b_1, b_2[ \subset \mathbb{R}, \, \, (b_1,b_2) \in \mathbb{R}^2\).
Find \(u \in L^{\infty}(0,T;H^2(\Omega))\) and \(v \in L^{\infty}(0,T;H^2(\Omega))\) such that,
\[
\begin{equation}
\label{eq:heterogenousCompetition}
\left\{
\begin{array}{ll}
&u_t = D_u \Delta u + r_u g_u(x) \, u(1-u-v \frac{g_v(x)}{g_u(x)}), \quad \forall (x,t) \in \Omega \times \mathbb{R}_{+}^{*} \\
&v_t = D_v \Delta v + r_v g_v(x) \, v(1-v-u \frac{g_u(x)}{g_v(x)}), \quad \forall (x,t) \in \Omega \times \mathbb{R}_{+}^{*} \\
&u(x,0) = u_0(x) \in C^{\infty}(\Omega), \\
&v(x,0) = v_0(x) \in C^{\infty}(\Omega), \\
&\frac{\partial u}{\partial n}(x,t) = 0, \quad \forall (x,t) \in \partial \Omega \times \mathbb{R}_{+} \\
&\frac{\partial v}{\partial n}(x,t) = 0, \quad \forall (x,t) \in \partial \Omega \times \mathbb{R}_{+}
\end{array}
\right.
\end{equation}
\]
where \(g_u \in C^{\infty}(\Omega)\) and \(g_v\in C^{\infty}(\Omega)\) are positive and representing the adaptation of the u and v population for all \(x \in \Omega\).
Here is the report (in French) and you can see below some of its figures.

(green : Perforatus perforatus, yellow : Chtamalus sp.)
(Pictures from Google Maps & Angelo Ciambelli).
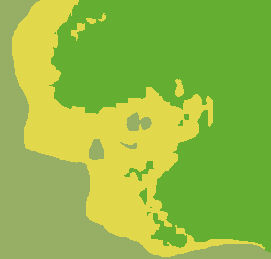
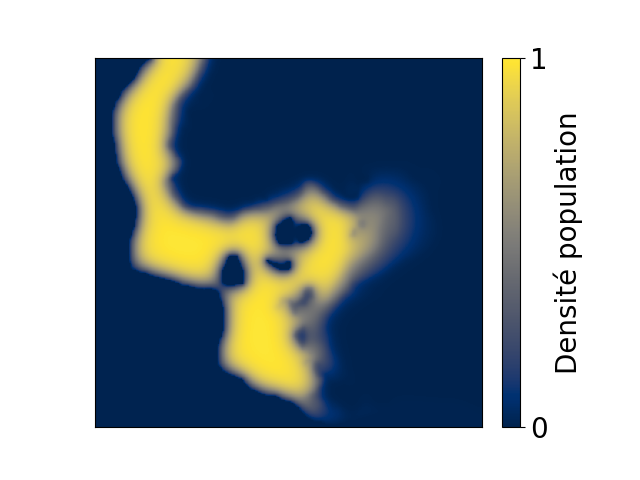
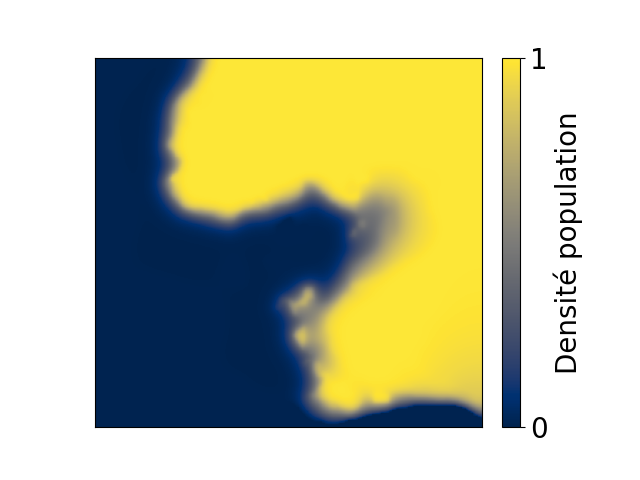
Repartition fronts geometry (Early 2024)
In biology I love to work on populations repartitions and dynamics and more precisely, on what is dictating their spatial or temporal distributions. Obvious drivers of distribution fronts are the environmental conditions. More precisely, physical properties and biological repartitions of other species that interact directly or indirectly with the species of interest. But, are there geometrical constants in the repartition coming from the species and environmental niches dynamics and characteristics ? An example of questions I currently work on is, "Are repartition fronts becoming more and more irregular, with increasing environmental changes ?" Such phenomenon might impact allele transmission in genetically heterogeneous populations by increasing allele mixing. I am trying to test this hypothesis with simulations recently using cellular automata and PDEs. More results may come soon.
At first the environment is favorable for the yellow-ish species and then become gradually
more favorable for the orange specie. Some image smoothing was used (median smoothing).

"la nuit étoilée" from Vincent Van Gogh.
Sailing ship simulation and optimal routing (February 2024)
This project was conducted during a group project at the "Ecole Nationale Supérieure de Techniques Avancées" (ENSTA Paris). Yanis Jouanaud and I coded a C++ program to firstly compute trajectory simulations of a sailing boat in constant wind and current field and to secondly find an optimal path to a zone of interest. The project was very successful, if one want to use the code, it can be found on my Github. See here.
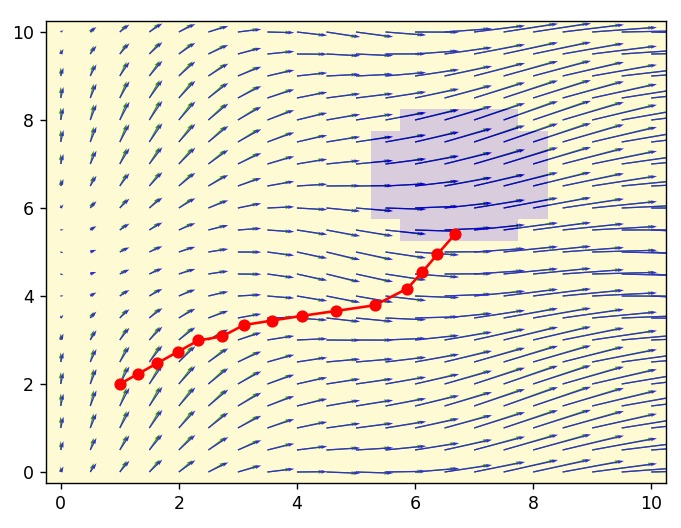
Green and blue arrows represent respectively the wind and current vector fields.
Gelatinous zooplankton diversity, distribution and seasonality
in the northern Barents Sea and Arctic Ocean (August 2022 - May 2023)
This project was my master thesis for my Msc degree in Arctic Marine Ecology at the Arctic University of Norway. It was part of the national Norwegian project Nansen Legacy that aimed to improve our knowledge of Arctic Ecosystems. I carried out the data analysis, DNA analysis and interpretation of the results for the gelatinous zooplankton. My supervisors were Camilla Svensen, Anette Wold and Sanna Majaneva. Respectively researchers at the Arctic University of Norway (UiT), the Norwegian Polar institute (NPI) and the Norwegian University of Science and Technology (NTNU). My thesis report is published here, and some results are to be published in a manuscript with my supervisors soon.